Tăng tốc huấn luyện mô hình AI với phương pháp Gradient Descent

Nội dung

1. Giới thiệu

Trong Machine Learning, việc đánh giá hiệu suất của một mô hình là bước quan trọng để đảm bảo rằng mô hình hoạt động tốt trên dữ liệu thực tế. Các chỉ số đo lường hiệu suất như Accuracy, Sensitivity (Recall) và Specificity là những công cụ phổ biến được sử dụng để đánh giá khả năng phân loại của mô hình.

Accuracy đo lường tỷ lệ dự đoán đúng trên tổng số dự đoán, thể hiện mức độ chính xác tổng thể của mô hình. Tuy nhiên, khi dữ liệu bị mất cân bằng (ví dụ số lượng lớp không đồng đều), chỉ số này có thể không phản ánh đúng hiệu suất của mô hình.
Sensitivity (hay Recall) đánh giá khả năng của mô hình trong việc phát hiện các mẫu thuộc lớp dương tính. Nó đặc biệt quan trọng trong các bài toán mà việc phát hiện đúng các trường hợp dương tính là ưu tiên hàng đầu, như chẩn đoán bệnh tật.
Specificity thì ngược lại với Sensitivity, tập trung vào khả năng mô hình loại bỏ các trường hợp âm tính một cách chính xác. Điều này rất hữu ích trong các trường hợp mà việc nhận diện đúng lớp âm tính có tầm quan trọng cao, như trong các bài toán kiểm tra chất lượng sản phẩm.

Hiểu rõ và áp dụng đúng các chỉ số này giúp người phát triển mô hình tối ưu hóa và lựa chọn mô hình phù hợp với bài toán cụ thể.

2. Confusion Matrix

Confusion Matrix là một công cụ dùng để đánh giá hiệu suất của một mô hình phân loại. Nó hiển thị số lần mô hình dự đoán đúng và sai cho từng lớp, giúp bạn dễ dàng hiểu rõ mô hình phân loại chính xác hay sai lệch như thế nào.

Confusion Matrix là một bảng hình vuông với các giá trị thể hiện kết quả của mô hình phân loại:

	Predicted Positive	Predicted Negative
Actual Positive	True Positive (TP)	False Negative (FN)
Actual Negative	False Positive (FP)	True Negative (TN)

Giải thích các thành phần

True Positive (TP): Số mẫu thực sự dương tính và được mô hình dự đoán chính xác là dương tính.
True Negative (TN): Số mẫu thực sự âm tính và được mô hình dự đoán chính xác là âm tính.
False Positive (FP): Số mẫu thực sự âm tính nhưng mô hình lại dự đoán nhầm là dương tính.
False Negative (FN): Số mẫu thực sự dương tính nhưng mô hình lại dự đoán nhầm là âm tính.

Ví dụ về Confusion Matrix

Giả sử bạn có một mô hình phân loại nhị phân với kết quả như sau:

Số mẫu thực sự dương tính: 50
Số mẫu thực sự âm tính: 50
Mô hình dự đoán chính xác 45 mẫu dương tính và 40 mẫu âm tính.
Các kết quả nhầm lẫn là 5 False Negative và 10 False Positive.

Confusion Matrix sẽ như sau:

	Predicted Positive	Predicted Negative
Actual Positive	45 (TP)	5 (FN)
Actual Negative	10 (FP)	40 (TN)

Trong đó:

TP (True Positive): Số lượng dự đoán đúng cho lớp dương tính.
TN (True Negative): Số lượng dự đoán đúng cho lớp âm tính.
FP (False Positive): Số lượng dự đoán sai cho lớp dương tính (âm tính bị dự đoán nhầm thành dương tính).
FN (False Negative): Số lượng dự đoán sai cho lớp âm tính (dương tính bị dự đoán nhầm thành âm tính).

3. Accuracy

Accuracy là một trong những chỉ số phổ biến nhất được sử dụng để đo lường hiệu suất của các mô hình phân loại. Nó biểu thị tỷ lệ phần trăm các dự đoán đúng so với tổng số mẫu dữ liệu được dự đoán.

Công thức Accuracy

Công thức tính độ chính xác (Accuracy) như sau:

$A c c u r a c y = \frac{T P + T N}{T P + T N + F P + F N}$

Ví dụ về Accuracy

Giả sử chúng ta có 100 mẫu dữ liệu, trong đó mô hình dự đoán đúng 90 mẫu và sai 10 mẫu. Khi đó, độ chính xác (Accuracy) sẽ là:

$A c c u r a c y = \frac{90}{100} = 0.9 = 90 %$

Độ chính xác và dữ liệu mất cân bằng

Mặc dù Accuracy là một chỉ số quan trọng, nhưng nó có thể không phản ánh đúng hiệu suất của mô hình trong các bài toán mà dữ liệu bị mất cân bằng. Ví dụ, nếu mô hình chỉ dự đoán tất cả các mẫu thuộc một lớp, độ chính xác vẫn có thể cao nếu lớp đó chiếm tỷ lệ lớn trong dữ liệu.

Chương trình mẫu tính Accuracy với pytorch:

Đoạn code dưới đây minh họa cách tính độ chính xác trong PyTorch:

import torch

# Hàm tính độ chính xác
def accuracy(preds, labels):
    # Lấy số dự đoán chính xác
    correct = (preds == labels).sum().item()
    # Tính độ chính xác
    acc = correct / labels.size(0)
    return acc

# Ví dụ về dự đoán và nhãn thực tế
predictions = torch.tensor([1, 0, 1, 1, 0])
labels = torch.tensor([1, 0, 1, 0, 0])

# Tính độ chính xác
acc = accuracy(predictions, labels)
print(f'Accuracy: {acc * 100:.2f}%')

Trong ví dụ trên, ta có 5 mẫu với dự đoán và nhãn thực tế. Hàm accuracy sẽ tính toán độ chính xác dựa trên số lượng dự đoán đúng so với tổng số mẫu.

Kết quả đoạn chương trình mẫu trên là: Accuracy: 80.00%

4. Precision

Precision là một chỉ số đánh giá hiệu suất của mô hình phân loại, đặc biệt chú trọng đến tính chính xác của các dự đoán dương tính. Nó biểu thị tỷ lệ mẫu dương tính được dự đoán đúng trên tổng số mẫu được mô hình dự đoán là dương tính.

Công thức Precision

Công thức tính độ chính xác theo lớp dương (Precision) như sau:

$P r e c i s i o n = \frac{T P}{T P + F P}$

Trong đó:

TP (True Positive): Số lượng dự đoán đúng cho lớp dương tính.
FP (False Positive): Số lượng dự đoán sai cho lớp dương tính (âm tính bị dự đoán nhầm thành dương tính).

Ví dụ về Precision

Giả sử mô hình dự đoán 30 mẫu là dương tính, trong đó có 25 mẫu đúng và 5 mẫu sai. Khi đó, độ chính xác theo lớp dương (Precision) sẽ được tính như sau:

$P r e c i s i o n = \frac{25}{25 + 5} = \frac{25}{30} = 0.83 = 83 %$

Precision đặc biệt quan trọng trong các bài toán mà việc dự đoán sai lớp dương tính (False Positive) có hậu quả nghiêm trọng. Ví dụ, trong chẩn đoán bệnh, nếu mô hình dự đoán một người bệnh khi họ thực sự không mắc bệnh, điều này có thể dẫn đến việc điều trị không cần thiết. Do đó, chỉ số Precision giúp giảm thiểu các trường hợp dự đoán sai lớp dương tính.

Chương trình mẫu tính Precision với pytorch:

Đoạn code dưới đây minh họa cách tính Precision trong PyTorch:

import torch

# Hàm tính Precision
def precision(preds, labels):
    # Tính True Positive (TP) và False Positive (FP)
    true_positive = ((preds == 1) & (labels == 1)).sum().item()
    false_positive = ((preds == 1) & (labels == 0)).sum().item()
    
    # Tính Precision
    if true_positive + false_positive == 0:
        return 0
    else:
        prec = true_positive / (true_positive + false_positive)
        return prec

# Ví dụ về dự đoán và nhãn thực tế
predictions = torch.tensor([1, 0, 1, 1, 0])
labels = torch.tensor([1, 0, 1, 0, 0])

# Tính Precision
prec = precision(predictions, labels)
print(f'Precision: {prec * 100:.2f}%')

Trong ví dụ trên, mô hình có 5 dự đoán và nhãn thực tế tương ứng. Hàm precision sẽ tính toán tỷ lệ True Positive trên tổng số mẫu được dự đoán là dương tính.

Kết quả đoạn chương trình mẫu trên: Precision: 66.67%

Precision rất quan trọng trong các bài toán mà việc dự đoán sai lớp dương tính có thể gây ra hậu quả lớn, chẳng hạn như phát hiện gian lận, chẩn đoán y tế, hoặc lọc spam.

5. Recall

Recall, còn được gọi là Sensitivity hoặc True Positive Rate, là một chỉ số quan trọng để đánh giá khả năng của mô hình trong việc nhận diện đúng các mẫu thuộc lớp dương tính. Nó thể hiện tỷ lệ các mẫu dương tính thực sự được mô hình dự đoán đúng trên tổng số mẫu dương tính trong tập dữ liệu.

Công thức Recall

Công thức tính Recall (Độ nhạy) như sau:

$R e c a l l = \frac{T P}{T P + F N}$

Trong đó:

TP (True Positive): Số lượng dự đoán đúng cho lớp dương tính.
FN (False Negative): Số lượng dự đoán sai cho lớp dương tính (dương tính bị dự đoán nhầm thành âm tính).

Ví dụ về Recall

Giả sử có 50 mẫu thực sự thuộc lớp dương tính, và mô hình dự đoán đúng 40 mẫu, trong khi bỏ sót 10 mẫu (False Negative). Khi đó, Recall được tính như sau:

$R e c a l l = \frac{40}{40 + 10} = \frac{40}{50} = 0.8 = 80 %$

Recall đặc biệt quan trọng trong các bài toán mà việc bỏ sót các trường hợp dương tính (False Negative) có hậu quả nghiêm trọng. Ví dụ, trong chẩn đoán y tế, việc bỏ sót một bệnh nhân mắc bệnh (FN) có thể gây ra những rủi ro lớn. Vì vậy, trong những trường hợp này, Recall được ưu tiên cao hơn so với Precision.

Chương trình mẫu tính Recall với pytorch:

Đoạn code dưới đây minh họa cách tính Recall trong PyTorch:

import torch

# Hàm tính Recall
def recall(preds, labels):
    # Tính True Positive (TP) và False Negative (FN)
    true_positive = ((preds == 1) & (labels == 1)).sum().item()
    false_negative = ((preds == 0) & (labels == 1)).sum().item()
    
    # Tính Recall
    if true_positive + false_negative == 0:
        return 0
    else:
        rec = true_positive / (true_positive + false_negative)
        return rec

# Ví dụ về dự đoán và nhãn thực tế
predictions = torch.tensor([1, 0, 1, 1, 0])
labels = torch.tensor([1, 0, 1, 0, 1])

# Tính Recall
rec = recall(predictions, labels)
print(f'Recall: {rec * 100:.2f}%')

Trong ví dụ trên, ta có các giá trị dự đoán và nhãn thực tế. Hàm recall sẽ tính toán tỷ lệ True Positive trên tổng số mẫu dương tính thực sự, để đánh giá khả năng của mô hình trong việc phát hiện đúng các trường hợp dương tính.

Kết quả đoạn chương trình mẫu trên: Recall: 66.67%

Trong các bài toán như chẩn đoán bệnh, phát hiện gian lận, hoặc các tình huống liên quan đến bảo mật, Recall là một chỉ số đặc biệt quan trọng vì nó giúp đảm bảo rằng hầu hết các trường hợp cần phát hiện sẽ không bị bỏ sót.

6. F1-Score

F1-Score là một chỉ số tổng hợp giữa Precision (Độ chính xác theo lớp dương) và Recall (Độ nhạy), đặc biệt hữu ích trong các bài toán phân loại mất cân bằng dữ liệu. F1-Score cung cấp một cái nhìn cân bằng giữa Precision và Recall, khi việc tối ưu hóa cả hai chỉ số này là cần thiết. Nó được tính bằng trung bình điều hòa của Precision và Recall.

Công thức F1-Score

Công thức tính F1-Score như sau:

$F 1 = 2 \times \frac{P r e c i s i o n \times R e c a l l}{P r e c i s i o n + R e c a l l}$

Trong đó:

Precision: Tỷ lệ dự đoán đúng cho lớp dương tính trên tổng số mẫu được dự đoán là dương tính.
Recall: Tỷ lệ mẫu dương tính thực sự được dự đoán đúng.

Ví dụ về F1-Score

Giả sử mô hình của bạn có Precision là 80% và Recall là 70%. Khi đó, F1-Score được tính như sau:

$F 1 = 2 \times \frac{0.8 \times 0.7}{0.8 + 0.7} = 2 \times \frac{0.56}{1.5} = 0.7467 \approx 74.67 %$

F1-Score là chỉ số quan trọng khi có sự đánh đổi giữa Precision và Recall. Trong những tình huống mà bạn muốn cân bằng giữa việc giảm False Positive (FP) và False Negative (FN), F1-Score cung cấp một cái nhìn toàn diện hơn so với chỉ sử dụng riêng Precision hay Recall.

Chương trình mẫu tính F1-Score với pytorch:

Đoạn code dưới đây minh họa cách tính F1-Score trong PyTorch:

import torch

# Hàm tính Precision
def precision(preds, labels):
    true_positive = ((preds == 1) & (labels == 1)).sum().item()
    false_positive = ((preds == 1) & (labels == 0)).sum().item()
    if true_positive + false_positive == 0:
        return 0
    return true_positive / (true_positive + false_positive)

# Hàm tính Recall
def recall(preds, labels):
    true_positive = ((preds == 1) & (labels == 1)).sum().item()
    false_negative = ((preds == 0) & (labels == 1)).sum().item()
    if true_positive + false_negative == 0:
        return 0
    return true_positive / (true_positive + false_negative)

# Hàm tính F1-Score
def f1_score(preds, labels):
    prec = precision(preds, labels)
    rec = recall(preds, labels)
    if prec + rec == 0:
        return 0
    return 2 * (prec * rec) / (prec + rec)

# Ví dụ về dự đoán và nhãn thực tế
predictions = torch.tensor([1, 0, 1, 1, 0])
labels = torch.tensor([1, 0, 1, 0, 1])

# Tính F1-Score
f1 = f1_score(predictions, labels)
print(f'F1-Score: {f1 * 100:.2f}%')

Trong ví dụ trên, chúng ta tính toán F1-Score dựa trên các giá trị Precision và Recall. Hàm f1_score trả về trung bình điều hòa giữa Precision và Recall để cho ra chỉ số F1.

Kết quả đoạn chương trình trên: F1-Score: 66.67%

F1-Score đặc biệt quan trọng trong các bài toán mà dữ liệu mất cân bằng, nơi việc tối ưu hóa cả Precision lẫn Recall là cần thiết. Nó giúp cung cấp cái nhìn tổng quan về khả năng phân loại chính xác của mô hình trong những tình huống mà một chỉ số đơn lẻ không đủ phản ánh hiệu suất toàn diện.

7. ROC và AUC

ROC (Receiver Operating Characteristic) là một biểu đồ thể hiện hiệu suất của mô hình phân loại ở các ngưỡng khác nhau. ROC Curve giúp so sánh giữa tỷ lệ True Positive (TPR) và False Positive (FPR), cung cấp một cái nhìn toàn diện về khả năng phân loại của mô hình đối với các lớp khác nhau.

ROC Curve và AUC

Đường cong ROC được tạo ra bằng cách vẽ True Positive Rate (TPR) so với False Positive Rate (FPR) ở các ngưỡng phân loại khác nhau. Tỷ lệ này được tính như sau:

True Positive Rate (TPR): Còn được gọi là Recall, được tính bằng công thức:
$T P R = \frac{T P}{T P + F N}$
False Positive Rate (FPR): Được tính bằng công thức:
$F P R = \frac{F P}{F P + T N}$

Kết quả là một đồ thị biểu diễn sự đánh đổi giữa TPR và FPR ở các ngưỡng khác nhau. Chỉ số phổ biến để đánh giá mô hình dựa trên ROC là AUC (Area Under the Curve), thể hiện diện tích dưới đường cong ROC. AUC nằm trong khoảng từ 0 đến 1, với giá trị càng gần 1 thì mô hình càng tốt.

Ví dụ về ROC và AUC

Giả sử bạn có một mô hình phân loại với nhiều ngưỡng dự đoán khác nhau. Ở mỗi ngưỡng, bạn tính toán TPR và FPR và vẽ đường ROC. Nếu đường ROC gần với góc trên bên trái của đồ thị (AUC gần bằng 1), thì mô hình của bạn hoạt động tốt.

Chương trình mẫu tính ROC và AUC với pytorch:

Dưới đây là đoạn code minh họa cách tính và vẽ ROC Curve, cũng như tính AUC bằng PyTorch và thư viện Scikit-learn:

import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression

# Tạo dữ liệu mẫu
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)

# Chia dữ liệu thành tập huấn luyện và tập kiểm tra
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Huấn luyện mô hình Logistic Regression
model = LogisticRegression()
model.fit(X_train, y_train)

# Dự đoán xác suất (probabilities) cho tập test
y_prob = model.predict_proba(X_test)[:, 1]

# Tính toán các giá trị FPR, TPR và thresholds
fpr, tpr, thresholds = roc_curve(y_test, y_prob)

# Tính diện tích dưới đường cong (AUC)
roc_auc = auc(fpr, tpr)

# Vẽ đồ thị ROC
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='blue', lw=2, label=f'ROC curve (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='gray', linestyle='--')

# Cấu hình đồ thị
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate (FPR)')
plt.ylabel('True Positive Rate (TPR)')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend(loc='lower right')

# Hiển thị đồ thị
plt.grid(True)
plt.show()

Trong ví dụ trên, mô hình dự đoán xác suất cho mỗi mẫu, và chúng ta sử dụng thư viện Scikit-learn để tính toán đường ROC và AUC. Kết quả được vẽ dưới dạng đồ thị để thể hiện mối quan hệ giữa TPR và FPR ở các ngưỡng khác nhau.

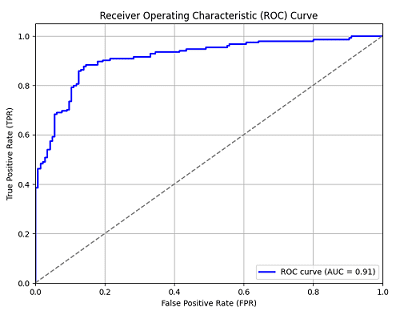
ROC và AUC là những công cụ mạnh mẽ giúp đánh giá khả năng phân loại của mô hình mà không phụ thuộc vào ngưỡng phân loại cụ thể. Điều này giúp ta có cái nhìn rõ ràng hơn về hiệu suất của mô hình trong các bài toán phân loại nhị phân.

8. Kết luận

Việc lựa chọn phương pháp đánh giá hiệu suất phù hợp là yếu tố quan trọng giúp cải thiện chất lượng mô hình Machine Learning. Tùy vào loại bài toán và dữ liệu, các chỉ số như Accuracy, Precision, Recall, F1-Score hay AUC-ROC đều mang đến những góc nhìn riêng về hiệu quả của mô hình. Để đảm bảo mô hình hoạt động tối ưu trong các tình huống thực tế, việc kết hợp nhiều phương pháp đánh giá và phân tích kết quả là cần thiết. Qua đó, bạn có thể đảm bảo rằng mô hình không chỉ hoạt động tốt trên dữ liệu huấn luyện mà còn có khả năng tổng quát hóa cao trên dữ liệu thực tế.

Xem thêm: Học AI toàn diện cùng AIcandy, Kiến thức nền tảng trí tuệ nhân tạo, Thực hành học máy và trí tuệ nhân tạo, Kho dữ liệu dành cho học máy, Bản tin AI, Công cụ AI