Khám phá K-nearest neighbors cho phân loại và hồi quy

Nội dung

1. Giới thiệu về K-nearest neighbors

K-nearest neighbors (KNN) là một trong những thuật toán học máy cơ bản nhất, nhưng vô cùng mạnh mẽ trong cả bài toán phân loại và hồi quy.

KNN là một thuật toán học máy không tham số (non-parametric) và học giám sát (supervised learning). Ý tưởng chính là tìm kiếm k điểm dữ liệu gần nhất trong tập huấn luyện, sau đó sử dụng chúng để dự đoán nhãn hoặc giá trị của điểm dữ liệu mới.

2. Nguyên lý hoạt động của KNN

2.1. Các bước thực hiện

Chọn giá trị của k

k là số lượng hàng xóm gần nhất sẽ được sử dụng.

Tính khoảng cách

Khoảng cách giữa điểm cần dự đoán và các điểm trong tập huấn luyện được tính toán. Khoảng cách Euclidean là phổ biến nhất:

\[d(x, y) = \sqrt{\sum_{i=1}^{n}(x_i – y_i)^2}\]

Chọn k hàng xóm gần nhất

Chọn ra k điểm gần nhất từ tập huấn luyện.

Dự đoán

Phân loại: Đưa ra nhãn của điểm mới dựa trên đa số phiếu từ k hàng xóm.
Hồi quy: Dự đoán giá trị liên tục bằng cách trung bình (hoặc trung bình có trọng số) của các giá trị hàng xóm.

2.2. Bài toán phân loại

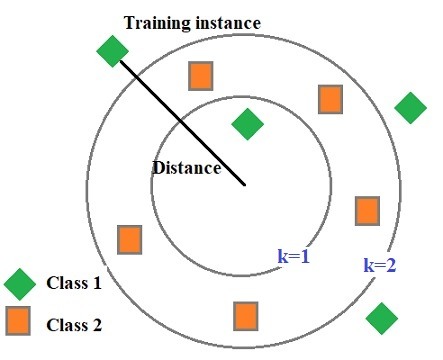
Trong bài toán phân loại, KNN hoạt động dựa trên nguyên lý đa số phiếu (majority voting). Ví dụ, giả sử có một tập dữ liệu với hai lớp, và chúng ta muốn phân loại một điểm mới với k = 3.

Giả sử ba hàng xóm gần nhất có nhãn lần lượt là {A, B, A}. Do lớp A xuất hiện nhiều hơn, nên điểm mới sẽ được phân vào lớp A.

Công thức tính đa số phiếu

Công thức tính xác suất P(A) cho một điểm mới thuộc lớp A:

\[P(A) = \frac{N_A}{k}\]

Trong đó, N_A là số lượng hàng xóm thuộc lớp A, k là tổng số hàng xóm (ở đây là 3).

Ví dụ thực tế với PyTorch

Dưới đây là ví dụ sử dụng PyTorch để triển khai KNN cho bài toán phân loại:

import torch
import torch.nn.functional as F
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

# Tạo dữ liệu giả
X, y = make_classification(n_samples=100, n_features=2, n_classes=2, n_clusters_per_class=1, n_informative=2)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# Chuyển đổi thành tensor
X_train = torch.tensor(X_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.int64)

def knn_classification(X_train, y_train, X_test, k):
    distances = torch.cdist(X_test, X_train)  # Tính khoảng cách giữa các điểm
    knn_idxs = distances.argsort()[:, :k]  # Lấy k hàng xóm gần nhất
    knn_labels = y_train[knn_idxs]  # Lấy nhãn của k hàng xóm gần nhất
    mode_labels, _ = torch.mode(knn_labels, dim=1)  # Lấy nhãn xuất hiện nhiều nhất
    return mode_labels

# Dự đoán với k=3
k = 3
y_pred = knn_classification(X_train, y_train, X_test, k)

# Tính độ chính xác
accuracy = torch.sum(y_pred == torch.tensor(y_test)).item() / len(y_test)
print(f"Accuracy: {accuracy * 100:.2f}%")

Trong ví dụ này, chúng ta tạo một tập dữ liệu giả lập với hai lớp. Sau đó, sử dụng hàm knn_classification để dự đoán nhãn của các điểm dữ liệu trong tập kiểm tra. Cuối cùng, tính độ chính xác của mô hình.

2.4. Bài toán hồi quy

Trong bài toán hồi quy, KNN dự đoán giá trị liên tục cho điểm mới dựa trên trung bình (hoặc trung bình có trọng số) của các giá trị thuộc hàng xóm gần nhất.

Công thức tính giá trị dự đoán

Giả sử giá trị cần dự đoán là y, và y_1, y_2, … y_k là giá trị của k hàng xóm gần nhất, giá trị dự đoán được tính theo công thức:

\[\hat{y} = \frac{1}{k} \sum_{i=1}^{k} y_i\]

Nếu sử dụng trung bình trọng số, giá trị dự đoán sẽ là:

\[\hat{y} = \frac{\sum_{i=1}^{k} w_i y_i}{\sum_{i=1}^{k} w_i}\]

Trong đó w_i là trọng số tương ứng với khoảng cách giữa điểm mới và hàng xóm thứ i.

Ví dụ thực tế với PyTorch

Dưới đây là ví dụ sử dụng PyTorch để triển khai KNN cho bài toán hồi quy:

import torch
import torch.nn.functional as F
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split

# Tạo dữ liệu giả
X, y = make_regression(n_samples=100, n_features=2, noise=0.1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# Chuyển đổi thành tensor
X_train = torch.tensor(X_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32)

def knn_regression(X_train, y_train, X_test, k):
    distances = torch.cdist(X_test, X_train)  # Tính khoảng cách giữa các điểm
    knn_idxs = distances.argsort()[:, :k]  # Lấy k hàng xóm gần nhất
    knn_values = y_train[knn_idxs]  # Lấy giá trị của k hàng xóm gần nhất
    mean_values = knn_values.mean(dim=1)  # Trung bình giá trị các hàng xóm
    return mean_values

# Dự đoán với k=3
k = 3
y_pred = knn_regression(X_train, y_train, X_test, k)

# Tính MSE
mse = F.mse_loss(y_pred, torch.tensor(y_test))
print(f"MSE: {mse:.4f}")

Ví dụ này minh họa cách sử dụng KNN để thực hiện hồi quy trên một tập dữ liệu giả lập. Kết quả dự đoán được so sánh với giá trị thực tế bằng cách tính toán Mean Squared Error (MSE).

3. Chọn giá trị của k

3.1. Tầm quan trọng của việc chọn giá trị k

Trong thuật toán KNN, giá trị k (số lượng hàng xóm gần nhất) là một tham số quan trọng quyết định hiệu suất của mô hình. Chọn k quá nhỏ có thể khiến mô hình trở nên quá nhạy cảm với các nhiễu và đặc điểm riêng của từng điểm dữ liệu, dẫn đến hiện tượng overfitting. Ngược lại, chọn k quá lớn có thể làm mất đi các chi tiết quan trọng trong dữ liệu, dẫn đến hiện tượng underfitting. Do đó, việc chọn k cần được thực hiện cẩn thận và dựa trên nhiều yếu tố khác nhau.

3.2. Ảnh hưởng của giá trị k đến hiệu suất mô hình

Giá trị k nhỏ (k = 1, 2, 3,…):

Khi k rất nhỏ, mô hình KNN chỉ dựa vào một hoặc một vài điểm gần nhất để dự đoán kết quả. Điều này có thể dẫn đến việc mô hình bị ảnh hưởng mạnh bởi các điểm dữ liệu nhiễu hoặc lỗi (outliers). Với k = 1, KNN trở thành một loại mô hình cực kỳ cục bộ, và dễ bị overfitting, tức là mô hình sẽ dự đoán rất tốt trên dữ liệu huấn luyện nhưng có thể dự đoán kém trên dữ liệu kiểm tra hoặc dữ liệu mới.

Giá trị k lớn:

Khi k tăng, mô hình trở nên tổng quát hơn vì nó sẽ xem xét nhiều điểm dữ liệu để đưa ra quyết định. Điều này giúp giảm thiểu ảnh hưởng của các điểm dữ liệu nhiễu, nhưng đồng thời cũng có nguy cơ làm mất đi các đặc điểm quan trọng của dữ liệu cục bộ. Nếu k quá lớn, mô hình có thể trở nên quá tổng quát (underfitting), dẫn đến việc dự đoán trở nên không chính xác vì nó không phản ánh đúng các mối quan hệ cục bộ trong dữ liệu.

3.3. Các phương pháp chọn giá trị k

Việc xác định giá trị k tối ưu có thể thực hiện thông qua một số phương pháp phổ biến:

Cross-validation

Cross-validation là phương pháp phổ biến nhất để chọn k. Với cross-validation, tập dữ liệu được chia thành nhiều phần (folds), và mô hình được huấn luyện trên một số phần trong khi kiểm tra trên phần còn lại. Quá trình này được lặp lại nhiều lần với các giá trị k khác nhau, và giá trị k tối ưu được chọn dựa trên hiệu suất trung bình trên tất cả các fold.
Cross-validation không chỉ giúp tìm ra giá trị k tốt nhất mà còn giúp đánh giá độ ổn định và khả năng tổng quát hóa của mô hình.

Nguyên tắc thumb rule (quy tắc ngón tay cái)

Một nguyên tắc thumb rule đơn giản để chọn k là chọn giá trị k bằng căn bậc hai của số lượng điểm dữ liệu trong tập huấn luyện: $\sqrt{n}$ Trong đó $n$ là số lượng mẫu trong tập huấn luyện. Đây là một phương pháp đơn giản và nhanh chóng để bắt đầu, nhưng nó không phải lúc nào cũng cho kết quả tối ưu. Thông thường, phương pháp này được sử dụng như một điểm khởi đầu, và sau đó giá trị k có thể được tinh chỉnh thông qua cross-validation hoặc các phương pháp khác.

Grid search

Grid search là một phương pháp hệ thống để tìm kiếm giá trị k tối ưu bằng cách thử tất cả các giá trị trong một khoảng được định trước. Ví dụ, bạn có thể thử các giá trị k từ 1 đến 20 và chọn giá trị có hiệu suất tốt nhất dựa trên một số chỉ số đánh giá như độ chính xác (accuracy), F1-score, hoặc mean squared error (MSE).
Grid search có thể kết hợp với cross-validation để đảm bảo rằng giá trị k chọn được không chỉ tốt trên tập dữ liệu hiện tại mà còn có khả năng tổng quát hóa tốt.

Random search

Random search là một phiên bản đơn giản hơn của grid search, trong đó các giá trị k được chọn ngẫu nhiên từ một khoảng giá trị nhất định. Random search thường ít tốn kém hơn về mặt tính toán so với grid search, và trong một số trường hợp có thể tìm được giá trị k tốt hơn hoặc gần tối ưu mà không cần phải kiểm tra tất cả các giá trị có thể.

Sử dụng phương pháp loại bỏ nhiễu

Khi dữ liệu chứa nhiều nhiễu, việc giảm ảnh hưởng của các điểm dữ liệu lỗi có thể giúp chọn k tốt hơn. Các kỹ thuật như loại bỏ các điểm dữ liệu nằm ngoài một khoảng xác định (outlier removal) hoặc giảm thiểu nhiễu bằng các phương pháp lọc trước khi áp dụng KNN có thể cải thiện việc chọn k.

3.4. Các yếu tố ảnh hưởng đến việc chọn giá trị k

Kích thước tập dữ liệu:

Kích thước của tập dữ liệu huấn luyện ảnh hưởng trực tiếp đến việc chọn k. Với tập dữ liệu lớn, giá trị k có thể lớn hơn để đảm bảo rằng dự đoán không bị ảnh hưởng quá nhiều bởi nhiễu. Ngược lại, với các tập dữ liệu nhỏ, k nhỏ hơn có thể phù hợp hơn.

Chiều của dữ liệu (Dimensionality):

Khi số lượng đặc trưng (features) của dữ liệu tăng lên, không gian dữ liệu trở nên thưa thớt hơn, và khoảng cách giữa các điểm dữ liệu trở nên ít phân biệt hơn (hiện tượng “curse of dimensionality”). Trong trường hợp này, một giá trị k lớn có thể cần thiết để giảm thiểu ảnh hưởng của chiều cao dữ liệu.

Phân phối dữ liệu:

Phân phối của dữ liệu cũng là một yếu tố quan trọng. Nếu dữ liệu có các cụm riêng biệt (clusters), một giá trị k nhỏ có thể giúp phát hiện các cụm này một cách chính xác hơn. Ngược lại, nếu dữ liệu phân phối ngẫu nhiên, k lớn hơn có thể mang lại kết quả tốt hơn.

3.5. Tối ưu hóa giá trị k cho từng bài toán cụ thể

Bài toán phân loại

Trong bài toán phân loại, việc chọn k phù hợp giúp cân bằng giữa việc duy trì sự chính xác của mô hình và khả năng tổng quát hóa cho dữ liệu mới. Một giá trị k tối ưu sẽ giúp mô hình nhận dạng đúng các lớp và giảm thiểu lỗi phân loại.

Bài toán hồi quy

Đối với bài toán hồi quy, việc chọn k không chỉ ảnh hưởng đến độ chính xác của dự đoán mà còn quyết định mức độ “mượt” của các dự đoán. Giá trị k quá nhỏ có thể dẫn đến các dự đoán biến động mạnh, trong khi k quá lớn có thể làm mất đi sự nhạy cảm của mô hình với các thay đổi nhỏ trong dữ liệu.

4. Ưu và nhược điểm của KNN trong hồi quy

4.1. Ưu điểm

Dễ hiểu và dễ triển khai

KNN là một trong những thuật toán đơn giản nhất trong học máy. Không cần xây dựng mô hình phức tạp hoặc tìm kiếm các tham số phức tạp, KNN chỉ dựa vào tính toán khoảng cách và tìm kiếm k hàng xóm gần nhất.
Điều này làm cho KNN trở nên dễ dàng để hiểu và triển khai, ngay cả đối với những người mới bắt đầu trong lĩnh vực học máy.

Không yêu cầu giả định về phân phối dữ liệu

KNN không dựa vào bất kỳ giả định nào về phân phối của dữ liệu, điều này rất hữu ích trong các trường hợp mà bạn không biết rõ về hình dạng của dữ liệu.
Điều này đặc biệt quan trọng khi dữ liệu có tính chất phi tuyến tính hoặc không tuân theo các phân phối thông thường (như phân phối chuẩn).

Linh hoạt với các loại dữ liệu khác nhau

KNN có thể áp dụng cho nhiều loại dữ liệu khác nhau, từ dữ liệu số, dữ liệu phân loại đến dữ liệu dạng văn bản hoặc hình ảnh, chỉ cần có một cách để đo khoảng cách giữa các điểm dữ liệu.
Điều này làm cho KNN trở thành một lựa chọn linh hoạt trong các ứng dụng đa dạng từ khoa học dữ liệu đến kỹ thuật phần mềm.

Không cần giai đoạn huấn luyện

KNN không yêu cầu huấn luyện mô hình trước khi sử dụng; toàn bộ quá trình diễn ra trong quá trình dự đoán. Điều này có thể tiết kiệm thời gian khi xử lý các tập dữ liệu nhỏ hoặc vừa phải.
Ngoài ra, KNN có thể thích ứng nhanh chóng với những thay đổi trong dữ liệu mà không cần huấn luyện lại toàn bộ mô hình.

4.2. Nhược điểm

Độ phức tạp tính toán cao

KNN cần phải tính toán khoảng cách giữa điểm dữ liệu mới và tất cả các điểm trong tập huấn luyện, điều này dẫn đến độ phức tạp tính toán là $O (n)$ , với $n$ là số lượng điểm trong tập huấn luyện.
Khi số lượng mẫu hoặc chiều của dữ liệu lớn, việc tính toán này trở nên rất tốn kém về thời gian và tài nguyên, khiến KNN không phù hợp với các ứng dụng yêu cầu thời gian thực hoặc xử lý dữ liệu lớn.

Nhạy cảm với nhiễu và dữ liệu không liên quan

KNN rất nhạy cảm với nhiễu (noise) trong dữ liệu, đặc biệt là các điểm dữ liệu lỗi (outliers) hoặc các đặc trưng không liên quan.
Nếu dữ liệu chứa nhiều nhiễu, các điểm này có thể được coi là hàng xóm gần nhất và gây ảnh hưởng đến kết quả dự đoán, dẫn đến sai số cao hơn. Điều này yêu cầu phải có bước tiền xử lý dữ liệu kỹ lưỡng trước khi áp dụng KNN.

Lựa chọn giá trị k khó khăn

Việc chọn đúng giá trị k là rất quan trọng nhưng không phải lúc nào cũng đơn giản. Giá trị k quá nhỏ có thể dẫn đến overfitting, nơi mô hình dự đoán rất tốt trên tập huấn luyện nhưng kém trên dữ liệu mới.
Ngược lại, giá trị k quá lớn có thể dẫn đến underfitting, nơi mô hình trở nên quá tổng quát và mất đi tính đặc trưng của các điểm dữ liệu gần kề. Để giải quyết vấn đề này, các kỹ thuật như cross-validation thường được sử dụng, nhưng điều này lại tăng thêm độ phức tạp và chi phí tính toán.

Khó mở rộng cho dữ liệu lớn

Do đặc tính phải lưu trữ toàn bộ tập dữ liệu huấn luyện và tính toán khoảng cách cho mỗi dự đoán, KNN không dễ dàng mở rộng cho các tập dữ liệu lớn. Điều này có thể gây ra các vấn đề về bộ nhớ và hiệu suất, đặc biệt là khi triển khai trong các hệ thống thực tế.
Ngoài ra, khi làm việc với dữ liệu có số lượng lớn đặc trưng (high-dimensional data), KNN có thể gặp phải hiện tượng “curse of dimensionality”, nơi khoảng cách giữa các điểm dữ liệu trở nên gần như bằng nhau, làm giảm hiệu quả của thuật toán.

5. Ứng dụng của KNN trong thực tế

5.1. Phân loại văn bản

KNN là một trong những thuật toán phổ biến nhất được sử dụng trong lĩnh vực phân loại văn bản. Với khả năng xử lý dữ liệu phi cấu trúc như văn bản, KNN có thể được áp dụng vào nhiều ứng dụng khác nhau, bao gồm:

Phân loại tài liệu (Document Classification):

Trong phân loại tài liệu, KNN có thể được sử dụng để gán nhãn cho các văn bản dựa trên nội dung của chúng. Ví dụ, KNN có thể giúp phân loại tài liệu thành các thể loại như thể thao, chính trị, công nghệ, v.v. bằng cách so sánh văn bản cần phân loại với các văn bản đã biết nhãn trước đó.
Khi sử dụng KNN cho phân loại văn bản, các đặc trưng (features) thường được biểu diễn dưới dạng vector từ (word vectors) hoặc sử dụng phương pháp TF-IDF để cân nhắc tần suất từ và tầm quan trọng của chúng trong văn bản.

Phát hiện thư rác (Spam Detection):

KNN cũng được sử dụng rộng rãi trong việc phát hiện thư rác. Thuật toán này có thể phân loại email là thư rác hay không dựa trên các đặc trưng của email như tần suất xuất hiện của từ ngữ, tiêu đề email, hoặc các từ khóa đặc biệt liên quan đến thư rác.
Khi áp dụng vào phát hiện thư rác, KNN có thể tận dụng các tập dữ liệu lớn từ các email đã được phân loại trước đó, và qua đó học cách nhận diện các mẫu thư rác mới một cách hiệu quả.

5.2. Nhận dạng hình ảnh

Nhận dạng hình ảnh là một trong những lĩnh vực mà KNN được sử dụng rất phổ biến, đặc biệt trong các ứng dụng yêu cầu độ chính xác cao và khả năng phản ứng nhanh:

Nhận dạng khuôn mặt (Face Recognition):

KNN được sử dụng trong hệ thống nhận dạng khuôn mặt để phân loại và nhận diện các hình ảnh khuôn mặt. Khi một hình ảnh khuôn mặt mới được cung cấp, KNN sẽ tìm kiếm trong tập dữ liệu các khuôn mặt đã biết để xác định khuôn mặt nào có đặc điểm tương tự nhất.
Các đặc trưng của khuôn mặt thường được trích xuất sử dụng các kỹ thuật xử lý hình ảnh hoặc các mô hình học sâu, sau đó sử dụng KNN để so sánh các đặc trưng này và đưa ra quyết định nhận dạng.

Nhận dạng chữ viết tay (Handwritten Digit Recognition):

KNN cũng được sử dụng trong nhận dạng chữ viết tay, một ứng dụng phổ biến trong các hệ thống nhận dạng chữ số như kiểm tra bài thi trắc nghiệm tự động hoặc xử lý tài liệu số hóa. Trong ứng dụng này, KNN sẽ so sánh hình ảnh chữ số viết tay với các hình ảnh mẫu đã biết để xác định chữ số đó.
Ví dụ nổi tiếng nhất là việc sử dụng KNN trên tập dữ liệu MNIST, một tập dữ liệu tiêu chuẩn gồm các chữ số viết tay từ 0 đến 9, nơi KNN đã chứng tỏ là một phương pháp đơn giản nhưng hiệu quả trong việc phân loại các chữ số này.

5.3. Dự đoán trong lĩnh vực tài chính

Trong lĩnh vực tài chính, KNN có nhiều ứng dụng khác nhau, từ dự đoán giá cổ phiếu đến phân tích rủi ro và quản lý danh mục đầu tư:

Dự đoán giá cổ phiếu (Stock Price Prediction):

Mặc dù các phương pháp dự đoán cổ phiếu phức tạp như mạng nơ-ron hoặc mô hình chuỗi thời gian thường được sử dụng, KNN vẫn có thể được áp dụng để dự đoán giá cổ phiếu bằng cách xem xét các đặc điểm tương tự giữa các ngày giao dịch.
KNN có thể sử dụng thông tin từ các ngày giao dịch trước để dự đoán giá cổ phiếu vào ngày hiện tại hoặc tương lai gần bằng cách tìm kiếm các ngày có các đặc điểm tương tự (như giá mở cửa, giá đóng cửa, khối lượng giao dịch) và dự đoán dựa trên các ngày đó.

Phân tích rủi ro tín dụng (Credit Risk Analysis):

Trong phân tích rủi ro tín dụng, KNN có thể được sử dụng để phân loại khách hàng thành các nhóm rủi ro khác nhau dựa trên hồ sơ tín dụng của họ. Các đặc trưng có thể bao gồm lịch sử tín dụng, thu nhập, nợ nần, và các thông tin nhân khẩu học khác.
Khi một khách hàng mới yêu cầu tín dụng, KNN sẽ so sánh họ với các khách hàng trước đó trong cùng nhóm rủi ro và dự đoán khả năng trả nợ của họ dựa trên kết quả của những khách hàng tương tự.

5.4. Y tế và chẩn đoán bệnh

KNN cũng có ứng dụng rộng rãi trong lĩnh vực y tế, đặc biệt trong việc hỗ trợ chẩn đoán bệnh và phân loại các loại bệnh:

Chẩn đoán bệnh dựa trên hình ảnh y tế (Medical Image Diagnosis):

Trong y tế, KNN có thể được sử dụng để phân loại các hình ảnh y tế, chẳng hạn như hình ảnh X-quang, MRI, hoặc siêu âm. Ví dụ, KNN có thể giúp phân loại các khối u trong hình ảnh X-quang thành lành tính hoặc ác tính dựa trên các đặc điểm hình ảnh.
KNN đặc biệt hữu ích khi dữ liệu về các trường hợp bệnh lý tương tự có sẵn, giúp mô hình học từ những trường hợp trước đó để dự đoán kết quả của các trường hợp mới.

Dự đoán bệnh tiểu đường (Diabetes Prediction):

KNN có thể được sử dụng để dự đoán khả năng mắc bệnh tiểu đường dựa trên các đặc điểm sinh học như tuổi tác, chỉ số BMI, huyết áp, và các thông số khác. Bằng cách so sánh bệnh nhân mới với các bệnh nhân đã biết tình trạng bệnh, KNN có thể ước tính xác suất mắc bệnh của họ.
Trong ứng dụng này, KNN cần một tập dữ liệu lớn và đa dạng để đảm bảo rằng các dự đoán có độ chính xác cao, đặc biệt khi phân tích trên các nhóm dân số khác nhau.

5.5. Phân tích thị trường và đề xuất sản phẩm

Trong thương mại điện tử và phân tích thị trường, KNN có thể được sử dụng để phân tích hành vi người tiêu dùng và đề xuất các sản phẩm phù hợp:

Hệ thống gợi ý sản phẩm (Product Recommendation Systems):

KNN được sử dụng trong các hệ thống gợi ý để đề xuất sản phẩm cho người dùng dựa trên lịch sử mua sắm hoặc duyệt web của họ. Ví dụ, một hệ thống có thể gợi ý các sản phẩm tương tự như những gì người dùng đã mua hoặc xem trước đó bằng cách tìm kiếm các người dùng có hành vi tương tự.
Hệ thống gợi ý dựa trên KNN thường sử dụng các đặc trưng như lịch sử giao dịch, tần suất mua hàng, hoặc điểm số xếp hạng sản phẩm để đưa ra các gợi ý có tính cá nhân hóa cao.

Phân đoạn thị trường (Market Segmentation):

Trong phân đoạn thị trường, KNN có thể được sử dụng để nhóm các khách hàng thành các phân khúc khác nhau dựa trên hành vi mua sắm, sở thích, và các đặc điểm nhân khẩu học khác. Điều này giúp các công ty tạo ra các chiến lược tiếp thị và sản phẩm phù hợp với từng phân khúc khách hàng.
Các đặc trưng phổ biến trong phân đoạn thị trường bao gồm thu nhập, độ tuổi, khu vực địa lý, tần suất mua sắm, và loại sản phẩm ưa thích.

6. Kết luận

KNN là một thuật toán mạnh mẽ và linh hoạt, có thể được áp dụng cho nhiều bài toán phân loại và hồi quy khác nhau. Mặc dù có một số hạn chế như độ phức tạp tính toán cao và nhạy cảm với nhiễu, KNN vẫn là lựa chọn tốt khi cần một phương pháp đơn giản, dễ hiểu và có thể triển khai nhanh chóng.

Để triển khai KNN hiệu quả, cần phải lựa chọn giá trị k một cách cẩn thận và đảm bảo rằng dữ liệu đã được tiền xử lý tốt để loại bỏ các đặc trưng không liên quan hoặc nhiễu.

Hy vọng rằng bài viết này sẽ giúp bạn hiểu rõ hơn về KNN và có thể áp dụng thành công vào các dự án học máy của mình!