Phân loại dữ liệu (Data classification): Tìm hiểu chi tiết

Nội dung

1. Giới thiệu

Phân loại dữ liệu là một kỹ thuật quan trọng trong học máy (machine learning) và trí tuệ nhân tạo, giúp chia các đối tượng hoặc mẫu dữ liệu vào các nhóm hoặc nhãn cụ thể. Phân loại được sử dụng rộng rãi trong nhiều ứng dụng thực tế, chẳng hạn như phân loại email (spam và không spam), nhận diện khuôn mặt, chẩn đoán y khoa và nhiều hơn nữa.

Quá trình phân loại bao gồm việc xây dựng một mô hình dựa trên tập dữ liệu huấn luyện, sau đó sử dụng mô hình này để dự đoán nhãn cho các dữ liệu mới. Các mô hình phân loại phổ biến như phân loại nhị phân, phân loại đa lớp, phân loại nhiều nhãn, phân loại thứ tự, phân loại chuỗi thời gian, phân loại đồ thị.

2. Phân loại nhị phân (Binary Classification)

2.1. Giới thiệu

Phân loại nhị phân là trường hợp đơn giản nhất của phân loại, nơi dữ liệu được phân thành hai nhóm. Ví dụ, trong một hệ thống phát hiện email spam, mỗi email sẽ được phân loại vào một trong hai nhóm: “spam” hoặc “không spam”.

2.2. Mô hình toán học

Mô hình phân loại nhị phân có thể được biểu diễn bằng hàm tuyến tính như sau:

\[
y = \sigma(\mathbf{w}^\top \mathbf{x} + b)
\]

Trong đó:

$\mathbf{x}$ là vector đặc trưng của mẫu dữ liệu.
$\mathbf{w}$ là vector trọng số của mô hình.
$b$ là hằng số điều chỉnh (bias).
$\sigma(z) = \frac{1}{1 + e^{-z}}$ là hàm sigmoid, dùng để chuẩn hóa đầu ra thành xác suất từ 0 đến 1.

2.3. Ứng dụng với pytorch

Dưới đây là một ví dụ đơn giản về cách xây dựng mô hình phân loại nhị phân bằng PyTorch cho bài toán XOR, một ví dụ điển hình trong học máy:

import torch
import torch.nn as nn
import torch.optim as optim

# Tạo dữ liệu XOR
data = torch.tensor([[0.0, 0.0], [0.0, 1.0], [1.0, 0.0], [1.0, 1.0]])
labels = torch.tensor([[0], [1], [1], [0]])  # Nhãn cho dữ liệu XOR

# Định nghĩa mô hình phân loại nhị phân
class BinaryClassifier(nn.Module):
    def __init__(self):
        super(BinaryClassifier, self).__init__()
        self.layer = nn.Linear(2, 1)  # Lớp đầu vào có 2 đặc trưng, đầu ra có 1 nhãn

    def forward(self, x):
        return torch.sigmoid(self.layer(x))

model = BinaryClassifier()

# Định nghĩa tiêu chí tổn thất và trình tối ưu hóa
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)

# Huấn luyện mô hình
for epoch in range(1000):
    optimizer.zero_grad()  # Xóa các gradient trước đó
    outputs = model(data)
    loss = criterion(outputs, labels.float())
    loss.backward()  # Tính gradient
    optimizer.step()  # Cập nhật trọng số

# Kiểm tra kết quả
with torch.no_grad():
    outputs = model(data)
    predicted = (outputs > 0.5).float()
    accuracy = (predicted == labels).float().mean()
    print(f'Accuracy: {accuracy.item() * 100}%')

Trong ví dụ này, chúng ta xây dựng một mô hình đơn giản để phân loại dữ liệu XOR thành hai lớp. Dữ liệu XOR là một ví dụ kinh điển, nơi mô hình tuyến tính đơn giản không thể phân loại chính xác. Tuy nhiên, với lớp kết nối đầy đủ và hàm kích hoạt sigmoid, mô hình có thể học cách phân loại đúng sau khi được huấn luyện.

3. Phân loại đa lớp (Multiclass Classification)

3.1. Giới thiệu

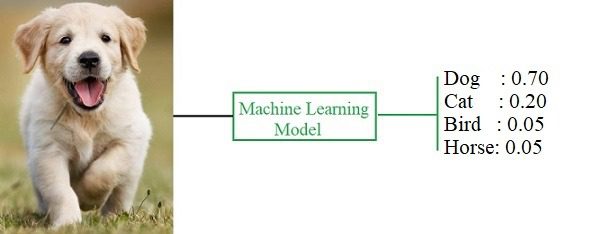
Phân loại đa lớp là một mở rộng của phân loại nhị phân, nơi dữ liệu có thể được phân loại vào nhiều nhóm hoặc nhãn khác nhau. Ví dụ, trong bài toán phân loại hình ảnh, chúng ta có thể cần phân loại các bức ảnh thành nhiều loại khác nhau, chẳng hạn như “mèo”, “chó”, “chim”.

3.2. Mô hình toán học

Hàm mất mát được sử dụng phổ biến nhất trong phân loại đa lớp là Cross-Entropy Loss, được định nghĩa như sau:

$$ L = – \sum_{i=1}^{C} y_i \log(\hat{y}_i) $$

Trong đó:

$C$ là số lượng các lớp (classes).
$y_i$ là nhãn thực tế (dạng one-hot).
$\hat{y}_i$ là xác suất dự đoán cho lớp $i$.

3.3. Ứng dụng với PyTorch

Dưới đây là ví dụ về cách xây dựng mô hình phân loại đa lớp bằng PyTorch:

import torch
import torch.nn as nn
import torch.optim as optim

# Tạo dữ liệu giả
data = torch.tensor([[1, 2], [2, 3], [3, 4], [4, 5], [5, 6]], dtype=torch.float)
labels = torch.tensor([0, 1, 2, 0, 1])  # Các lớp (classes) là 0, 1, 2

# Định nghĩa mô hình phân loại đa lớp
class MulticlassClassifier(nn.Module):
    def __init__(self):
        super(MulticlassClassifier, self).__init__()
        self.layer = nn.Linear(2, 3)  # Lớp đầu ra có 3 lớp

    def forward(self, x):
        return torch.softmax(self.layer(x), dim=1)

model = MulticlassClassifier()

# Định nghĩa tiêu chí tổn thất và trình tối ưu hóa
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)

# Huấn luyện mô hình
for epoch in range(1000):
    optimizer.zero_grad()
    outputs = model(data)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

# Kiểm tra kết quả
with torch.no_grad():
    outputs = model(data)
    _, predicted = torch.max(outputs, 1)
    accuracy = (predicted == labels).float().mean()
    print(f'Accuracy: {accuracy.item() * 100}%')

Trong ví dụ này, mô hình phân loại đa lớp dự đoán lớp của các mẫu dữ liệu giả định. Dữ liệu được gán vào ba lớp khác nhau, và mô hình được huấn luyện để tối ưu hóa hàm mất mát Cross-Entropy. Sau khi huấn luyện, chúng ta có thể kiểm tra độ chính xác của mô hình bằng cách so sánh dự đoán với nhãn thực tế.

4. Phân loại nhiều nhãn (Multi-label Classification)

4.1. Giới thiệu

Phân loại nhiều nhãn là trường hợp mà mỗi mẫu dữ liệu có thể được gán vào nhiều nhãn cùng một lúc. Điều này khác với phân loại đa lớp, nơi mỗi mẫu chỉ được gán vào một lớp. Ví dụ, một bài báo có thể được gán nhiều nhãn như “thể thao”, “bóng đá”, và “quốc tế”.

4.2. Mô hình toán học

Mô hình phổ biến cho phân loại nhiều nhãn là huấn luyện một bộ phân loại nhị phân cho từng nhãn một cách độc lập. Cho từng nhãn $ l $, ta xây dựng một hàm phân loại nhị phân
\[f_l: \mathbb{R}^d \rightarrow \{0, 1\} \]

với:

$ f_l(x) = 1 $ nếu mẫu $ x $ thuộc về lớp $ l $.
$ f_l(x) = 0 $ nếu mẫu $ x $ không thuộc về lớp $ l $.

Do đó, mô hình phân loại nhiều nhãn có thể được biểu diễn dưới dạng:

$ \hat{Y} = f(x) = \left\{ l \in \{1, 2, \dots, L\} \mid f_l(x) = 1 \right\} $

4.3. Ứng dụng với PyTorch

Dưới đây là ví dụ về cách xây dựng mô hình phân loại nhiều nhãn bằng PyTorch:

import torch
import torch.nn as nn
import torch.optim as optim

# Tạo dữ liệu giả
data = torch.tensor([[0.5, 1.5], [2.5, 3.5], [3.5, 4.5], [4.5, 5.5], [5.5, 6.5]])
labels = torch.tensor([[1, 0, 1], [0, 1, 1], [1, 1, 0], [0, 0, 1], [1, 1, 1]])  # Mỗi mẫu có thể thuộc nhiều nhãn

# Định nghĩa mô hình phân loại nhiều nhãn
class MultiLabelClassifier(nn.Module):
    def __init__(self):
        super(MultiLabelClassifier, self).__init__()
        self.layer = nn.Linear(2, 3)  # 3 nhãn đầu ra

    def forward(self, x):
        return torch.sigmoid(self.layer(x))  # Sử dụng sigmoid cho phân loại nhiều nhãn

model = MultiLabelClassifier()

# Định nghĩa tiêu chí tổn thất và trình tối ưu hóa
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)

# Huấn luyện mô hình
for epoch in range(1000):
    optimizer.zero_grad()
    outputs = model(data)
    loss = criterion(outputs, labels.float())
    loss.backward()
    optimizer.step()

# Kiểm tra kết quả
with torch.no_grad():
    outputs = model(data)
    predicted = (outputs > 0.5).float()
    accuracy = (predicted == labels).float().mean()
    print(f'Accuracy: {accuracy.item() * 100}%')

Trong ví dụ này, mô hình phân loại nhiều nhãn có khả năng dự đoán nhiều nhãn cho mỗi mẫu dữ liệu. Chúng ta sử dụng hàm sigmoid để chuẩn hóa đầu ra thành xác suất cho mỗi nhãn, và hàm BCELoss được sử dụng để tối ưu hóa mô hình.

5. Phân loại thứ tự (Ordinal Classification)

5.1. Giới thiệu

Trong lĩnh vực học máy và trí tuệ nhân tạo, phân loại thứ tự (Ordinal Classification) là một phương pháp phân loại đặc biệt, nơi các nhãn (labels) không chỉ đơn thuần là các lớp riêng biệt mà còn có một thứ tự rõ ràng giữa chúng. Khác với phân loại đa lớp (multiclass classification), nơi các lớp không có thứ tự cố định, phân loại thứ tự đòi hỏi phải tôn trọng mối quan hệ thứ tự giữa các lớp. Điều này có nghĩa là các lớp có mối liên hệ về mặt định lượng, chẳng hạn như “thấp”, “trung bình”, và “cao”.

5.2. Mô hình toán học

Giả sử chúng ta có các lớp thứ tự $\{1, 2, \ldots, L\}$, nơi lớp 1 là thấp nhất và lớp $L$ là cao nhất. Để mô hình hóa bài toán phân loại thứ tự, ta thường sử dụng các mô hình hồi quy hoặc mô hình phân loại với một số điều chỉnh để phản ánh thứ tự của các lớp.

Hàm mất mát (Loss Function)

Hàm mất mát cho phân loại thứ tự có thể được định nghĩa để phản ánh thứ tự giữa các lớp. Một ví dụ là hàm mất mát độ chính xác trung bình (mean absolute error) giữa dự đoán và thực tế:

\[
\mathcal{L}(\theta) = \frac{1}{N} \sum_{i=1}^{N} \left| \hat{y}_i – y_i \right|
\]

Trong đó:

$\hat{y}_i$ là dự đoán của mô hình cho mẫu $i$.
$y_i$ là lớp thực tế của mẫu $i$, và nó được ánh xạ thành giá trị số để phản ánh thứ tự.

Hàm kích hoạt (Activation Function)

Các mô hình phân loại thứ tự có thể sử dụng hàm kích hoạt (activation function) như hàm softmax để dự đoán xác suất của từng lớp, sau đó áp dụng các điều chỉnh để phản ánh thứ tự. Hàm softmax cho xác suất của từng lớp được tính như sau:

\[
\hat{p}_l = \frac{e^{z_l}}{\sum_{k=1}^{L} e^{z_k}}
\]

Trong đó:

$z_l$ là đầu ra của mô hình cho lớp $l$.
$\hat{p}_l$ là xác suất dự đoán của lớp $l$.

Sử dụng mô hình hồi quy

Mô hình hồi quy thứ tự có thể được sử dụng để dự đoán điểm số hoặc giá trị liên tục cho mỗi mẫu, sau đó phân loại điểm số đó thành các lớp thứ tự. Ví dụ, một mô hình hồi quy có thể dự đoán một giá trị liên tục $y$, và sau đó giá trị này được ánh xạ vào lớp thứ tự bằng cách sử dụng các ngưỡng:

\[
\text{Class}(y) = \begin{cases}
1 & \text{nếu } y \leq \theta_1 \\
2 & \text{nếu } \theta_1 < y \leq \theta_2 \\ \vdots \\ L & \text{nếu } y > \theta_{L-1}
\end{cases}
\]

Trong đó:

$\theta_1, \theta_2, \ldots, \theta_{L-1}$ là các ngưỡng phân chia các lớp.

5.3. Ứng dụng với PyTorch

import torch
import torch.nn as nn
import torch.optim as optim

# Tạo dữ liệu giả định
data = torch.tensor([[1.0], [2.0], [3.0], [4.0], [5.0]])
labels = torch.tensor([0, 1, 2, 3, 4])  # Các nhãn theo thứ tự

# Định nghĩa mô hình phân loại thứ tự
class OrdinalClassifier(nn.Module):
    def __init__(self):
        super(OrdinalClassifier, self).__init__()
        self.layer = nn.Linear(1, 1)  # Đầu vào có 1 đặc trưng, đầu ra là giá trị thứ tự

    def forward(self, x):
        return self.layer(x)

model = OrdinalClassifier()

# Định nghĩa tiêu chí tổn thất và trình tối ưu hóa
criterion = nn.MSELoss()  # Mean Squared Error phù hợp với bài toán này
optimizer = optim.SGD(model.parameters(), lr=0.01)

# Huấn luyện mô hình
for epoch in range(1000):
    optimizer.zero_grad()
    outputs = model(data)
    loss = criterion(outputs.squeeze(), labels.float())
    loss.backward()
    optimizer.step()

# Kiểm tra kết quả
with torch.no_grad():
    outputs = model(data)
    predicted = torch.round(outputs).squeeze()
    accuracy = (predicted == labels.float()).float().mean()
    print(f'Accuracy: {accuracy.item() * 100}%')

Trong ví dụ này, chúng ta xây dựng một mô hình phân loại thứ tự đơn giản bằng cách sử dụng PyTorch. Dữ liệu đầu vào là các giá trị số thực, và các nhãn được biểu diễn bằng các giá trị thứ tự từ 0 đến 4. Chúng ta sử dụng hàm mất mát Mean Squared Error (MSE) để huấn luyện mô hình. Sau khi huấn luyện, mô hình có thể dự đoán giá trị thứ tự cho các mẫu dữ liệu mới.

6. Phân loại chuỗi thời gian (Time Series Classification)

6.1. Giới thiệu

Phân loại chuỗi thời gian (Time Series Classification) là một phương pháp phân loại trong lĩnh vực học máy, nơi dữ liệu đầu vào là các chuỗi thời gian, tức là một tập hợp các điểm dữ liệu được sắp xếp theo thứ tự thời gian. Các chuỗi thời gian có thể đại diện cho bất kỳ hiện tượng nào thay đổi theo thời gian, chẳng hạn như giá cổ phiếu, tín hiệu điện tâm đồ (ECG), hoặc dữ liệu cảm biến.

6.2. Phương pháp phân loại

Phân loại chuỗi thời gian có thể được thực hiện bằng nhiều phương pháp khác nhau, bao gồm:

Phương pháp dựa trên đặc trưng

Trích xuất các đặc trưng từ chuỗi thời gian, chẳng hạn như giá trị trung bình, độ lệch chuẩn, hoặc các chỉ số phức tạp hơn như các đặc trưng tần số, sau đó sử dụng các mô hình phân loại truyền thống như SVM hoặc Random Forest.

Phương pháp dựa trên mô hình

Sử dụng các mô hình như HMM (Hidden Markov Model) hoặc ARIMA (Autoregressive Integrated Moving Average) để phân tích và phân loại chuỗi thời gian.

Mạng nơ-ron hồi quy (Recurrent Neural Networks – RNNs)

RNNs, đặc biệt là LSTM (Long Short-Term Memory), là một trong những phương pháp hiện đại và hiệu quả nhất để phân loại chuỗi thời gian. Những mô hình này có khả năng học từ các chuỗi dữ liệu có độ dài biến đổi và ghi nhớ các thông tin quan trọng qua thời gian dài.

6.3. Ứng dụng với Pytorch

Một ví dụ thực tế về phân loại chuỗi thời gian là phân loại các tín hiệu điện tâm đồ (ECG) để chẩn đoán các bệnh tim mạch. Trong ví dụ dưới đây, chúng ta sẽ sử dụng PyTorch để xây dựng một mô hình RNN đơn giản nhằm phân loại các chuỗi thời gian thành các lớp khác nhau dựa trên các mẫu tín hiệu.

import torch
import torch.nn as nn
import torch.optim as optim

# Định nghĩa mô hình RNN cho phân loại chuỗi thời gian
class RNNClassifier(nn.Module):
    def __init__(self, input_size, hidden_size, num_layers, num_classes):
        super(RNNClassifier, self).__init__()
        self.hidden_size = hidden_size
        self.num_layers = num_layers
        self.rnn = nn.RNN(input_size, hidden_size, num_layers, batch_first=True)
        self.fc = nn.Linear(hidden_size, num_classes)

    def forward(self, x):
        h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)
        out, _ = self.rnn(x, h0)
        out = self.fc(out[:, -1, :])
        return out

# Các thông số mô hình
input_size = 1
hidden_size = 64
num_layers = 2
num_classes = 3

# Khởi tạo mô hình
model = RNNClassifier(input_size, hidden_size, num_layers, num_classes)

# Định nghĩa tiêu chí tổn thất và trình tối ưu hóa
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# Dữ liệu giả lập
data = torch.rand(100, 10, input_size)  # 100 chuỗi, mỗi chuỗi có 10 điểm, 1 đặc trưng
labels = torch.randint(0, num_classes, (100,))  # 100 nhãn từ 0 đến 2

# Huấn luyện mô hình
for epoch in range(500):
    optimizer.zero_grad()
    outputs = model(data)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

# Kiểm tra kết quả
with torch.no_grad():
    outputs = model(data)
    _, predicted = torch.max(outputs.data, 1)
    accuracy = (predicted == labels).float().mean()
    print(f'Accuracy: {accuracy.item() * 100}%')

Trong ví dụ này, chúng ta xây dựng một mô hình RNN đơn giản bằng cách sử dụng PyTorch để phân loại chuỗi thời gian. Mô hình RNN được sử dụng để học các mẫu trong chuỗi thời gian, với đầu vào là các chuỗi dữ liệu và đầu ra là lớp dự đoán. Sau khi huấn luyện, mô hình có thể được sử dụng để phân loại các chuỗi thời gian mới.

7. Phân loại Đồ thị (Graph Classification)

7.1. Giới thiệu

Phân loại đồ thị (Graph Classification) là một phương pháp trong học máy liên quan đến việc gán nhãn cho toàn bộ đồ thị. Đây là một bài toán quan trọng trong nhiều lĩnh vực, từ hóa học, sinh học đến khoa học xã hội, nơi các đối tượng nghiên cứu có thể được mô hình hóa dưới dạng đồ thị. Ví dụ, một phân tử có thể được biểu diễn dưới dạng đồ thị với các nguyên tử là các đỉnh (nodes) và các liên kết hóa học là các cạnh (edges).

7.2. Phương pháp phân loại

Có nhiều phương pháp để phân loại đồ thị, bao gồm:

Phương pháp dựa trên đặc trưng

Trích xuất các đặc trưng của đồ thị như số đỉnh, số cạnh, hoặc các chỉ số khác như độ tập trung (clustering coefficient), sau đó sử dụng các thuật toán học máy truyền thống như SVM hoặc Random Forest để phân loại.

Mạng nơ-ron đồ thị (Graph Neural Networks – GNNs)

GNNs là phương pháp hiện đại và mạnh mẽ để xử lý và phân loại đồ thị. Chúng học cách biểu diễn các đồ thị dưới dạng vector số (embedding) và sử dụng các vector này để thực hiện phân loại.

7.3. Ứng dụng với Pytorch

Một ví dụ thực tế về phân loại đồ thị là dự đoán tính chất hóa học của các phân tử trong hóa học. Mỗi phân tử có thể được biểu diễn dưới dạng một đồ thị, với các nguyên tử là các đỉnh và các liên kết hóa học là các cạnh. Mục tiêu là xây dựng một mô hình học máy có thể dự đoán các tính chất của phân tử dựa trên cấu trúc đồ thị của nó.

Dưới đây là một ví dụ sử dụng PyTorch Geometric, một thư viện mở rộng của PyTorch dành riêng cho việc xử lý đồ thị:

import torch
import torch.nn.functional as F
from torch_geometric.data import DataLoader
from torch_geometric.datasets import TUDataset
from torch_geometric.nn import GCNConv, global_mean_pool

# Định nghĩa mô hình GCN cho phân loại đồ thị
class GCN(torch.nn.Module):
    def __init__(self, num_node_features, num_classes):
        super(GCN, self).__init__()
        self.conv1 = GCNConv(num_node_features, 64)
        self.conv2 = GCNConv(64, 64)
        self.fc = torch.nn.Linear(64, num_classes)

    def forward(self, x, edge_index, batch):
        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = self.conv2(x, edge_index)
        x = global_mean_pool(x, batch)  # Áp dụng pooling để giảm số lượng các node thành 1 vector
        x = self.fc(x)
        return F.log_softmax(x, dim=1)

# Tải bộ dữ liệu MUTAG từ TUDataset
dataset = TUDataset(root='/tmp/MUTAG', name='MUTAG')

# Chia bộ dữ liệu thành các tập huấn luyện và kiểm tra
train_loader = DataLoader(dataset[:150], batch_size=32, shuffle=True)
test_loader = DataLoader(dataset[150:], batch_size=32, shuffle=False)

# Khởi tạo mô hình, tiêu chí tổn thất và trình tối ưu hóa
model = GCN(num_node_features=dataset.num_node_features, num_classes=dataset.num_classes)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

# Huấn luyện mô hình
model.train()
for epoch in range(100):
    for data in train_loader:
        optimizer.zero_grad()
        out = model(data.x, data.edge_index, data.batch)
        loss = F.nll_loss(out, data.y)
        loss.backward()
        optimizer.step()

# Kiểm tra mô hình
model.eval()
correct = 0
for data in test_loader:
    out = model(data.x, data.edge_index, data.batch)
    pred = out.argmax(dim=1)
    correct += (pred == data.y).sum().item()

accuracy = correct / len(test_loader.dataset)
print(f'Accuracy: {accuracy * 100:.2f}%')

Trong ví dụ này, chúng ta sử dụng PyTorch Geometric để xây dựng một mô hình GCN (Graph Convolutional Network) nhằm phân loại các đồ thị trong bộ dữ liệu MUTAG, một bộ dữ liệu phổ biến trong phân loại đồ thị. Mô hình GCN học cách biểu diễn các đồ thị dưới dạng các vector số và sử dụng các vector này để dự đoán lớp của đồ thị.

8. Kết luận

Phân loại dữ liệu là một trong những nhiệm vụ cốt lõi trong học máy, với ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Dựa trên tính chất và cấu trúc của dữ liệu, có nhiều loại phân loại khác nhau, mỗi loại đều có những đặc điểm và ứng dụng riêng:

Phân loại nhị phân

Đây là loại phân loại đơn giản nhất, nơi dữ liệu được chia thành hai lớp khác nhau. Nó thường được sử dụng trong các bài toán như phát hiện spam, phân loại email hoặc dự đoán bệnh tật.

Phân loại đa lớp

Khi có nhiều hơn hai lớp, bài toán trở thành phân loại đa lớp. Nó được ứng dụng rộng rãi trong nhận diện hình ảnh, phân loại văn bản, và nhiều bài toán khác trong thực tế.

Phân loại nhiều nhãn

Đây là khi một mẫu dữ liệu có thể thuộc về nhiều lớp cùng lúc. Ví dụ điển hình là trong phân loại ảnh, một bức ảnh có thể chứa nhiều đối tượng khác nhau như người, xe, động vật, và mỗi đối tượng đều là một nhãn.

Phân loại thứ tự

Phân loại thứ tự (Ordinal Classification) là khi các lớp có một thứ tự nhất định, ví dụ như mức độ hài lòng từ “Rất không hài lòng” đến “Rất hài lòng”. Điều này thường xuất hiện trong các bài toán khảo sát và phân tích dữ liệu khách hàng.

Phân loại chuỗi thời gian

Đối với dữ liệu mà các mẫu được sắp xếp theo thời gian, phân loại chuỗi thời gian giúp phát hiện các mẫu và xu hướng trong dữ liệu thay đổi theo thời gian, với ứng dụng trong y tế, tài chính, và IoT.

Phân loại đồ thị

Khi dữ liệu được biểu diễn dưới dạng đồ thị, phân loại đồ thị cho phép chúng ta phân tích các đối tượng có cấu trúc phức tạp như phân tử hóa học, mạng xã hội, hoặc hệ thống kết nối mạng.

Mỗi loại phân loại đều có những ưu và nhược điểm riêng, cũng như các phương pháp và kỹ thuật phù hợp. Việc chọn lựa loại phân loại và phương pháp phù hợp phụ thuộc vào bản chất của dữ liệu và mục tiêu của bài toán. Sự phát triển của các phương pháp học máy, đặc biệt là các mạng nơ-ron sâu, đã mở ra nhiều cơ hội mới trong việc xử lý và phân loại dữ liệu phức tạp, giúp cải thiện hiệu suất và khả năng dự đoán trong các ứng dụng thực tế.