Thuật toán Random Forest: Giải thích chi tiết và ứng dụng

1. Giới thiệu

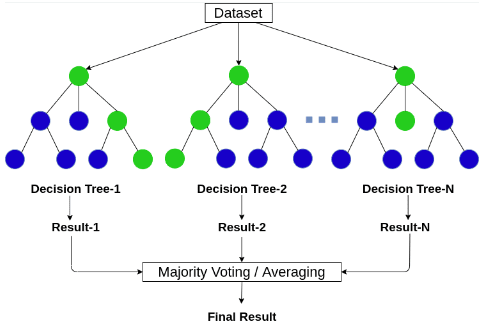
Random Forest là một thuật toán học máy thuộc nhóm học có giám sát (supervised learning) và được sử dụng phổ biến trong các bài toán phân loại (classification) và hồi quy (regression). Thuật toán này là một dạng của tập hợp học (ensemble learning), nơi mà nhiều mô hình yếu (weak learners), cụ thể là các cây quyết định (decision trees), được kết hợp lại để tạo thành một mô hình mạnh mẽ hơn.

Tại sao lại là “Random”?

Thuật ngữ “Random” trong Random Forest xuất phát từ hai yếu tố chính:

Ngẫu nhiên trong chọn mẫu

Thay vì sử dụng toàn bộ dữ liệu huấn luyện để xây dựng từng cây quyết định, thuật toán Random Forest chọn một mẫu ngẫu nhiên từ tập dữ liệu (với hoàn lại) để xây dựng mỗi cây. Kỹ thuật này được gọi là Bagging (Bootstrap Aggregating). Bagging giúp giảm thiểu phương sai của mô hình, cải thiện độ chính xác tổng thể.

Ngẫu nhiên trong chọn đặc trưng

Khi tạo các nút trong mỗi cây, chỉ một tập con ngẫu nhiên của tất cả các đặc trưng được xem xét để chọn đặc trưng tốt nhất tại mỗi bước. Điều này giúp các cây quyết định đa dạng hơn, giảm thiểu hiện tượng overfitting và đảm bảo rằng các cây không bị phụ thuộc quá mức vào một đặc trưng cụ thể nào đó.

2. Cơ chế hoạt động

2.1. Giới thiệu

Random Forest bao gồm nhiều cây quyết định (Decision Trees). Mỗi cây là một mô hình dự đoán độc lập và đưa ra một dự đoán. Đối với bài toán phân loại, Random Forest sẽ lấy kết quả dự đoán của từng cây và chọn kết quả nào xuất hiện nhiều nhất (majority vote). Đối với bài toán hồi quy, kết quả cuối cùng là giá trị trung bình của các dự đoán từ tất cả các cây.

Ví dụ, giả sử chúng ta có 100 cây quyết định. Đối với một mẫu mới, nếu 60 cây dự đoán rằng mẫu đó thuộc lớp A, và 40 cây dự đoán rằng mẫu đó thuộc lớp B, thì Random Forest sẽ dự đoán rằng mẫu đó thuộc lớp A (vì nó nhận được số phiếu cao hơn).

2.2. Công thức tổng quát

Một cây quyết định trong Random Forest thực hiện phân loại hoặc hồi quy bằng cách chia nhỏ không gian đặc trưng thành các vùng con. Các phân vùng này được xác định dựa trên các điều kiện phân tách tại mỗi nút trong cây. Giả sử có một đặc trưng \( X \) và một ngưỡng phân tách \( t \), việc phân tách tại một nút có thể được biểu diễn bằng cách chọn một hàm chỉ thị \( I \), trong đó:

\[I(X \leq t) \text{ và } I(X > t)
\]

Nếu đặc trưng \( X \) tại mẫu đó nhỏ hơn hoặc bằng \( t \), mẫu sẽ được chuyển đến nhánh trái; ngược lại, nó sẽ được chuyển đến nhánh phải. Quá trình này tiếp tục cho đến khi đạt đến một nút lá, nơi giá trị đầu ra của nút đó được sử dụng làm dự đoán.

2.3. Hàm mất mát và độ không thuần khiết

Quá trình xây dựng cây quyết định trong Random Forest liên quan đến việc tối ưu hóa một hàm mất mát, thường là giảm thiểu độ không thuần khiết (impurity) của các nút. Đối với bài toán phân loại, độ không thuần khiết thường được đo bằng chỉ số Gini hoặc entropy.

Chỉ số Gini

Chỉ số Gini là một cách đo lường độ không thuần khiết của một nút. Công thức tính chỉ số Gini cho một nút \( t \) là:

\[Gini(t) = 1 – \sum_{i=1}^{C} p_i^2\]

Trong đó, \( p_i \) là xác suất của việc một mẫu thuộc lớp \( i \) tại nút \( t \), và \( C \) là tổng số lớp. Một nút thuần khiết (tức là tất cả các mẫu đều thuộc một lớp) sẽ có chỉ số Gini bằng 0.

Entropy

Entropy là một thước đo khác về độ không thuần khiết, và nó được sử dụng trong việc xây dựng cây quyết định theo phương pháp ID3 hoặc C4.5. Công thức tính entropy tại một nút \( t \) là:

\[Entropy(t) = – \sum_{i=1}^{C} p_i \log_2(p_i)\]

Tương tự như chỉ số Gini, entropy đạt giá trị nhỏ nhất khi nút hoàn toàn thuần khiết.

Giảm độ không thuần khiết (Information Gain)

Khi một đặc trưng được chọn để phân tách tại một nút, mục tiêu là làm giảm độ không thuần khiết của các nút con so với nút cha. Sự giảm này, được gọi là Information Gain (đối với entropy) hoặc Gini Gain (đối với chỉ số Gini), được tính như sau:

\[\text{Information Gain} = \text{Impurity}(t) – \sum_{k \in \{left, right\}} \frac{N_k}{N} \text{Impurity}(t_k)\]

Trong đó:

• \( \text{Impurity}(t) \) là độ không thuần khiết tại nút cha.
• \( \text{Impurity}(t_k) \) là độ không thuần khiết tại các nút con sau khi phân tách.
• \( N \) là số lượng mẫu tại nút cha, và \( N_k \) là số lượng mẫu tại nút con \( k \).

2.4. Bagging và ngẫu nhiên hóa

Trong Random Forest, hai khía cạnh quan trọng của tính ngẫu nhiên giúp tăng cường khả năng tổng quát hóa của mô hình:

Bagging

Thuật toán Random Forest sử dụng phương pháp Bagging (Bootstrap Aggregating) để xây dựng mỗi cây quyết định. Thay vì sử dụng toàn bộ tập dữ liệu huấn luyện, mỗi cây được huấn luyện trên một mẫu ngẫu nhiên từ tập dữ liệu, với việc lấy mẫu có hoàn lại (tức là một mẫu có thể được chọn nhiều lần).

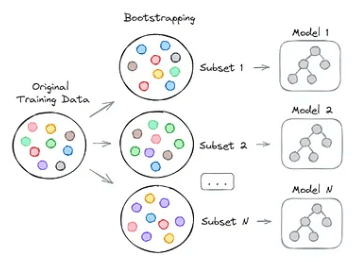
Ngẫu nhiên hóa đặc trưng

Tại mỗi bước chia tách trong cây, một tập con ngẫu nhiên của các đặc trưng được xem xét để tìm đặc trưng tốt nhất. Điều này làm cho mỗi cây  khác biệt hơn và giảm thiểu sự phụ thuộc vào một số đặc trưng cụ thể, từ đó giảm nguy cơ overfitting.

Công thức Bagging

Giả sử có \( B \) cây quyết định được xây dựng từ các bộ dữ liệu bootstrap khác nhau. Dự đoán của Random Forest đối với một mẫu mới \( x \) là:

Đối với bài toán phân loại:

$$\hat{y} = \text{majority_vote}\left(\hat{y}^{(1)}, \hat{y}^{(2)}, \dots, \hat{y}^{(B)}\right)$$

Đối với bài toán hồi quy:

\[\hat{y} = \frac{1}{B} \sum_{b=1}^{B} \hat{y}^{(b)}\]

Trong đó:

• \( \hat{y}^{(b)} \) là dự đoán của cây quyết định thứ \( b \) cho mẫu \( x \).
• \( B \) là tổng số cây.

2.5. Đánh giá mức độ quan trọng của đặc trưng

Trong Random Forest, mức độ quan trọng của các đặc trưng được đánh giá dựa trên mức giảm độ không thuần khiết (impurity) mà đặc trưng đó đóng góp khi được chọn làm đặc trưng phân tách. Đối với mỗi cây, tổng mức giảm impurity trên toàn bộ cây được tính cho mỗi đặc trưng, và sau đó được trung bình hóa qua tất cả các cây trong rừng.

Một cách khác để đánh giá tầm quan trọng của đặc trưng là sử dụng phương pháp Permuted Feature Importance, trong đó các giá trị của một đặc trưng cụ thể được xáo trộn ngẫu nhiên và mức giảm trong độ chính xác của mô hình được sử dụng để đánh giá mức độ quan trọng của đặc trưng đó.

Tóm lại, mức độ quan trọng của một đặc trưng \( X_j \) có thể được tính bằng công thức:

\[\text{Feature Importance}(X_j) = \frac{1}{B} \sum_{b=1}^{B} \sum_{t \in \text{nodes}} \Delta I(t)\]

Trong đó:

• \( \Delta I(t) \) là mức giảm impurity tại nút \( t \) khi sử dụng đặc trưng \( X_j \).
• \( B \) là tổng số cây trong rừng.
• \( \text{nodes} \) là tập hợp các nút trong cây \( b \) nơi \( X_j \) được sử dụng.

2.6. Out-of-Bag Error

Một đặc điểm nổi bật của Random Forest là khả năng ước tính lỗi dự đoán mà không cần tách riêng một tập dữ liệu kiểm tra, thông qua khái niệm lỗi Out-of-Bag (OOB). Trong quá trình huấn luyện, khoảng một phần ba mẫu trong mỗi bootstrap không được sử dụng để huấn luyện cây và do đó, có thể được sử dụng như một tập kiểm tra tự nhiên.

Lỗi OOB được tính bằng cách đánh giá mô hình trên các mẫu này, sau đó tính toán trung bình lỗi trên tất cả các cây:

\[\text{OOB Error} = \frac{1}{N} \sum_{i=1}^{N} I(\hat{y}_{OOB}(i) \neq y_i)\]

Trong đó:

• \(\hat{y}_{OOB}(i)\) là dự đoán của mô hình cho mẫu \(i\) khi mẫu này là out-of-bag cho cây mà dự đoán này được thực hiện.
• \(y_i\) là giá trị thực tế của mẫu \(i\).
• \(N\) là tổng số mẫu trong tập dữ liệu.
• \(I(\cdot)\) là hàm chỉ thị, nhận giá trị 1 nếu điều kiện trong ngoặc đơn là đúng và 0 nếu điều kiện là sai.

Ví dụ sử dụng python để tính toán OOB:

from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Tạo dữ liệu giả lập
X, y = make_classification(n_samples=1000, n_features=20, n_informative=10, n_classes=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Xây dựng mô hình Random Forest với lỗi OOB
model = RandomForestClassifier(n_estimators=100, oob_score=True, random_state=42)
model.fit(X_train, y_train)

# Tính toán độ chính xác OOB
oob_error = 1 - model.oob_score_
print(f'OOB Error: {oob_error:.4f}')

3. Ứng dụng 

Random Forest được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau nhờ vào tính chính xác và khả năng tổng quát hóa tốt. Dưới đây là một số ứng dụng tiêu biểu:

3.1. Phân loại và phát hiện gian lận (Fraud Detection)

Trong lĩnh vực tài chính, Random Forest được sử dụng để phát hiện các giao dịch gian lận. Ví dụ, các giao dịch thẻ tín dụng có thể được phân loại dựa trên các đặc trưng như số tiền giao dịch, tần suất giao dịch, địa điểm giao dịch, và lịch sử giao dịch trước đó. Random Forest có khả năng phát hiện những giao dịch bất thường và đưa ra cảnh báo về khả năng gian lận.

3.2. Y tế và chuẩn đoán bệnh

Trong y học, Random Forest hỗ trợ chuẩn đoán bệnh bằng cách phân loại các bệnh nhân dựa trên các triệu chứng và kết quả xét nghiệm. Ví dụ, đối với bệnh ung thư, Random Forest có thể sử dụng các đặc trưng như kích thước khối u, mật độ tế bào, và các yếu tố di truyền để dự đoán liệu một khối u có ác tính hay không.

Ví dụ khác, trong dự đoán bệnh tiểu đường, Random Forest có thể sử dụng các chỉ số như mức đường huyết lúc đói, chỉ số khối cơ thể (BMI), và tiền sử gia đình để dự đoán khả năng mắc bệnh.

3.3. Dự đoán thị trường chứng khoán

Random Forest được ứng dụng trong phân tích và dự đoán xu hướng thị trường chứng khoán. Bằng cách xử lý các dữ liệu lịch sử giá cổ phiếu, thông tin kinh tế, và các chỉ số kỹ thuật, Random Forest có thể dự đoán xu hướng tăng giảm của cổ phiếu hoặc chỉ số thị trường. Điều này có thể giúp các nhà đầu tư đưa ra các quyết định giao dịch dựa trên các dự báo đáng tin cậy.

3.4. Phân tích hình ảnh và nhận dạng khuôn mặt

Trong thị giác máy tính, Random Forest được sử dụng để phân loại các đối tượng trong hình ảnh và nhận dạng khuôn mặt. Bằng cách phân tích các đặc trưng như màu sắc, kết cấu, và các điểm nổi bật, Random Forest có thể phân loại các đối tượng trong hình ảnh với độ chính xác cao. Trong nhận dạng khuôn mặt, thuật toán có thể xác định danh tính của một người dựa trên các đặc điểm khuôn mặt, ngay cả trong các điều kiện ánh sáng và góc độ khác nhau.

3.5. Dự báo thời tiết và khí hậu

Random Forest cũng được sử dụng trong các mô hình dự báo thời tiết và khí hậu. Thuật toán này giúp dự đoán nhiệt độ, lượng mưa, và các hiện tượng thời tiết khác dựa trên dữ liệu thu thập từ nhiều nguồn khác nhau. Random Forest có khả năng xử lý tốt dữ liệu không đồng nhất và phức tạp, chẳng hạn như dữ liệu vệ tinh và dữ liệu cảm biến từ các trạm khí tượng.

4. Ưu điểm và nhược điểm của Random Forest

4.1. Ưu điểm

Khả năng xử lý dữ liệu lớn

Random Forest có thể xử lý một lượng lớn dữ liệu với độ chính xác cao, ngay cả khi dữ liệu chứa nhiều nhiễu hoặc có sự phân bố không đồng đều.

Giảm thiểu overfitting

Bằng cách kết hợp nhiều cây quyết định, Random Forest giúp giảm thiểu hiện tượng overfitting, đặc biệt là khi các cây quyết định được huấn luyện trên các mẫu ngẫu nhiên khác nhau.

Khả năng xử lý dữ liệu mất mát

Thuật toán có thể hoạt động tốt ngay cả khi một phần dữ liệu bị thiếu, vì mỗi cây chỉ sử dụng một phần dữ liệu và các đặc trưng khác nhau.

Dễ dàng điều chỉnh và mở rộng

Số lượng cây trong Random Forest có thể dễ dàng điều chỉnh để cân bằng giữa độ chính xác và hiệu suất tính toán. Ngoài ra, thuật toán này có thể được mở rộng để xử lý các bài toán phân loại nhiều lớp hoặc hồi quy đa đầu ra.

4.2. Nhược điểm

Tính toán phức tạp

Random Forest yêu cầu nhiều tài nguyên tính toán hơn so với một số thuật toán khác do số lượng cây lớn và quá trình huấn luyện phức tạp.

Khó tối ưu hóa các siêu tham số

Việc tìm kiếm và tối ưu hóa các siêu tham số của Random Forest, chẳng hạn như số lượng cây, độ sâu tối đa của cây, và số lượng đặc trưng để phân tách tại mỗi nút, có thể là một quá trình tốn thời gian và phức tạp. Việc lựa chọn các siêu tham số tốt nhất thường yêu cầu thử nghiệm và điều chỉnh nhiều lần.

Kích thước mô hình lớn

Khi số lượng cây lớn, kích thước của mô hình Random Forest có thể trở nên rất lớn, đòi hỏi nhiều bộ nhớ để lưu trữ và quản lý.

5. Ứng dụng với PyTorch

Dưới đây là ví dụ về cách xây dựng một mô hình Random Forest đơn giản để phân loại dữ liệu sử dụng PyTorch và scikit-learn. Mặc dù PyTorch không có triển khai trực tiếp của Random Forest, chúng ta có thể sử dụng scikit-learn để xây dựng mô hình và sau đó chuyển dữ liệu vào PyTorch để huấn luyện và đánh giá.

5.1. Tạo dữ liệu giả lập

import torch
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

# Tạo dữ liệu giả lập
X, y = make_classification(n_samples=1000, n_features=20, n_informative=10, n_classes=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Chuyển đổi sang tensor
X_train = torch.tensor(X_train, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.long)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_test = torch.tensor(y_test, dtype=torch.long)

Ở bước này, chúng ta đã tạo ra một bộ dữ liệu giả lập với 1000 mẫu, mỗi mẫu có 20 đặc trưng, trong đó có 10 đặc trưng mang thông tin quan trọng cho việc phân loại. Dữ liệu sau đó được chia thành tập huấn luyện và tập kiểm tra với tỷ lệ 80-20.

5.2. Xây dựng mô hình

Random Forest không được tích hợp sẵn trong PyTorch, nhưng ta có thể sử dụng thư viện scikit-learn để xây dựng mô hình và sau đó chuyển dữ liệu vào PyTorch để huấn luyện.

from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score

# Xây dựng mô hình Random Forest
model = RandomForestClassifier(n_estimators=100, random_state=42)
model.fit(X_train.numpy(), y_train.numpy())

# Dự đoán trên tập kiểm tra
y_pred = model.predict(X_test.numpy())

# Đánh giá mô hình
accuracy = accuracy_score(y_test.numpy(), y_pred)
print(f'Accuracy: {accuracy:.4f}')

Trong ví dụ này, chúng ta đã xây dựng một mô hình Random Forest với 100 cây quyết định (n_estimators=100). Mô hình được huấn luyện trên tập dữ liệu huấn luyện và sau đó được kiểm tra trên tập dữ liệu kiểm tra. Cuối cùng, độ chính xác của mô hình được tính toán và in ra kết quả.

5.3. Tinh chỉnh mô hình

Chúng ta có thể cải thiện mô hình Random Forest bằng cách điều chỉnh các tham số như số lượng cây (n_estimators), độ sâu tối đa của mỗi cây (max_depth), và số lượng đặc trưng được xem xét khi chia tách (max_features). Ví dụ, ta có thể thử nghiệm với các giá trị khác nhau của max_depth để tìm ra độ sâu tối ưu cho mô hình.

# Tinh chỉnh mô hình với độ sâu tối đa là 10
model = RandomForestClassifier(n_estimators=100, max_depth=10, random_state=42)
model.fit(X_train.numpy(), y_train.numpy())

# Đánh giá mô hình
y_pred = model.predict(X_test.numpy())
accuracy = accuracy_score(y_test.numpy(), y_pred)
print(f'Accuracy with max_depth=10: {accuracy:.4f}')

Ở đây, chúng ta đã giới hạn độ sâu của mỗi cây trong rừng ở mức 10. Điều này có thể giúp giảm thiểu hiện tượng overfitting, đặc biệt là khi dữ liệu có nhiễu hoặc chứa các mẫu không đại diện.

6. Kết luận

Random Forest là một trong những thuật toán học máy mạnh mẽ và linh hoạt, phù hợp với nhiều loại bài toán khác nhau từ phân loại, hồi quy đến các bài toán phức tạp hơn như phát hiện gian lận hay phân tích hình ảnh. Mặc dù có một số hạn chế về tính phức tạp và khả năng giải thích, Random Forest vẫn được ưa chuộng nhờ vào khả năng xử lý dữ liệu lớn, giảm thiểu overfitting, và tính dễ dàng trong việc tinh chỉnh mô hình.

Với các ví dụ đã được trình bày, bạn có thể dễ dàng áp dụng Random Forest vào các bài toán thực tế của mình, sử dụng PyTorch và scikit-learn để triển khai và đánh giá mô hình.